Levenshtein 编辑距离

发表于

Levenshtein 距离

什么是Levenshtein距离?
Levenshtein距离是由俄罗斯科学家弗拉基米尔·莱文斯坦在1965年提出这个概念。

Levenshtein距离(莱文斯坦距离), 是编辑距离（edit distance）的一种。
指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

比如将kitten一字转成sitting, 有三步：

sitten （k→s）
sittin （e→i）
sitting （→g）

用途

  • 相似度检测
  • 拼写检查
  • 文本搜索 (Lucene/Solr)
  • NLP
  • 等等

实现

如果用朴素的递归方法实现, 需要O(3^n)的时间复杂度, 明显我们要进行一些优化, 动态规划是比较常用的方法.

假设字符串target有1~m个字符, 字符串str1有1~n个:

定义最优子问题

通过插入/删除/替换操作, 把str1转换为target字符串.
要想找到最短编辑距离, 即是str1[1~i]转换成target[1~j]所需要的最少编辑次数

确定状态转换方程

我们将str1[1~i]转换成target[1~j]所需要的最少编辑次数, 定义为状态d[i, j].

确定决策并写出状态转移方程

当target[j]等于str1[i]

d[i, j] = d[i, j] + 0;

当target[j]不等于str1[i]

d[i, j] = min(
    d[i, j-1] + 1,
    d[i-1, j] + 1,
    d[i-1, j-1] + 1
    )

寻找边界条件

当target是空字符串时, d[i, 0] = str1的长度
当str1是空字符串时, d[0, j] = target的长度

经过这几步, 就可以开始写代码实现了. 以下给出的是状态递推DP算法, 除此以外, 仍可以使用带记忆的递归算法.

实现

int getEditDistance(char[] target, char[] str1) {
    int[][] distance = new int[str1.length + 1][target.length + 1];
    for (int i = 0; i <= str1.length; i++) {
        distance[i][0] = i;
    }
    for (int j = 0; j <= target.length; j++) {
        distance[0][j] = j;
    }

    for (int j = 1; j <= target.length; j++) {
        for (int i = 1; i <= str1.length; i++) {
            if (str1[i - 1] == target[j - 1 ]) {
                distance[i][j] = distance[i - 1][j - 1];
            } else {
                int distanceInsert = distance[i][j - 1] + 1;
                int distanceDelete = distance[i - 1][j] + 1;
                int distanceEdit = distance[i - 1][j - 1] + 1;
                distance[i][j] = Math.min(
                        Math.min(distanceInsert, distanceDelete),
                        distanceEdit);
            }
        }
    }
    return distance[str1.length][target.length];
}

以snowy和sunny字符串做测试, 计算过程如下:

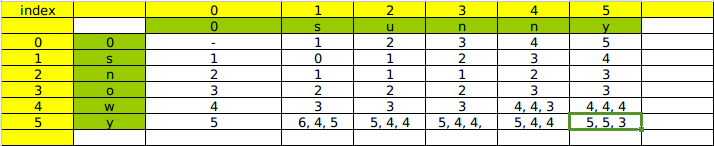
有三个值的, 分别是insert/delete/edit的计算距离, 最后得出最短编辑距离是3.

参考

莱文斯坦距离
[算法的乐趣 - C3 动态规划]