上一篇博客稳定匹配问题 - Gale & Shapley 我们介绍了稳定匹配的问题和Gale-Shapley算法, 这次我们尝试用二分图和匈牙利算法来解决问题.

二分图相关概念

首先了解一下二分图的相关概念, 假设有一个图G(V, E), V为顶点集合, 分为X和Y, 分别代表男人和女人, E为边集合, 边的两端分别在X和Y集合中.
我们规定G的子图Gs的边集合任意两条都不是同一顶点, 则Gs是一个匹配. 如图所示:

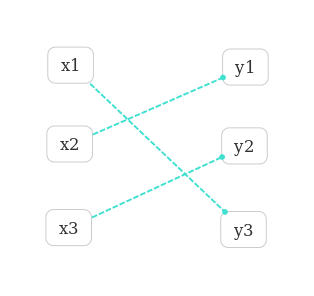
如果加上黑色边表示男女互相喜欢, 如下:

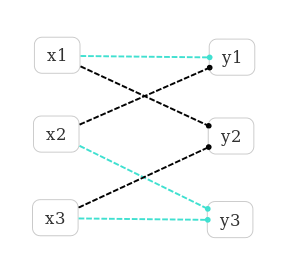
绿色边表示配对的结果, 称为匹配边, 其他称为非匹配边.
当匹配边最多时, 则称为该图的最大匹配.
接着介绍匈牙利算法.

匈牙利算法

接着是了解匈牙利算法, 在此之前, 我们先要知道几个概念:

增广路（augmenting path）:
从一个未匹配的点出发, 通过交替路(依次经过非匹配边、匹配边、非匹配边...依次交替的路径), 若途径其他未匹配点, 那么称为该交替路为增广路.
增广路有一个重要特点：非匹配边比匹配边多一条。所以取反(把增广路中的匹配边和非匹配边的身份交换)之后, 匹配边就比非匹配边多一条, 如此不断寻找增广路, 知道找不到增广路径时, 算法就结束了, 得到的就是最大匹配. 匈牙利算法就是这么做的.

算法实现

实现主要用到两个类: MatchRecord和HungaryAlgorithm.

MatchRecord 作为匹配过程的辅助记录, 比如边和点的关系/增广路等等, 如注释:


public class MatchRecord {
    // 男生/女生的人数
    int count;
    // 表示边 (用x和y坐标定位), 数值1表示两点存在边连接
    int edge[][];
    // 是否在当前增广路
    boolean onPath[];
    // 已找到的增广路
    int augmentPath[];
    // 最大匹配的结果数
    int maxMatch = 0;

    public MatchRecord(int count) {
        this.count = count;
    }

    public int getCount() {
        return count;
    }

    public void setOnPath(boolean[] onPath) {
        this.onPath = onPath;
    }

    public void setEdge(int[][] edge) {
        this.edge = edge;
    }

    public int[] getAugmentPath() {
        return augmentPath;
    }

    public void setAugmentPath(int[] augmentPath) {
        this.augmentPath = augmentPath;
    }

    public int getMaxMatch() {
        return maxMatch;
    }

    public int getEdge(int xi, int yi) {
        return this.edge[xi][yi];
    }

    public boolean notOnPath(int yi) {
        return ! onPath[yi];
    }

    public void setOnPath(int yi, boolean b) {
        this.onPath[yi] = true;
    }

    public int getAugmentPath(int yi) {
        return this.augmentPath[yi];
    }

    public void setAugmentPath(int yi, int xi) {
        this.augmentPath[yi] = xi;
    }

    public void reset() {
        int[] aug = new int[this.getCount()];
        for (int idx = 0; idx < aug.length; idx++) {
            aug[idx] = -1;
        }
        this.setOnPath(new boolean[this.getCount()]);
    }

    public void maxMatchInc() {
        this.maxMatch++;
    }
}

HungaryAlgorithm, 主要是执行匹配过程, 通过深度搜索来查找匹配:


public class HungaryAlgorithm {

    public static void main(String[] args) {
        MatchRecord rec = init();
        int count = rec.getCount();
        HungaryAlgorithm hungary = new HungaryAlgorithm();
        for (int xi = 0; xi < count; xi++) {
            if (hungary.findAugmentPath(rec, xi)) {
                rec.maxMatchInc();
            }
            rec.reset();
        }
        boolean found = rec.getMaxMatch() == count;
        if (found) {
            print(rec);
        }
    }

    // TODO 设置测试数据
    public static MatchRecord init() {
        int count = 3;
        int[][] edge = new int[][]{
                {1, 1, 0},
                {1, 0, 1},
                {0, 1, 1}
        };
        int[] augment = new int[count];
        for (int idx = 0; idx < augment.length; idx++) {
            augment[idx] = -1;
        }
        //
        MatchRecord rec = new MatchRecord(count);
        rec.setEdge(edge);
        rec.setOnPath(new boolean[count]);
        rec.setAugmentPath(augment);
        return rec;
    }

    public boolean findAugmentPath(MatchRecord matchRecord, int xi) {
        for (int yi = 0; yi < matchRecord.getCount(); yi++) {
            if (matchRecord.getEdge(xi, yi) == 1 && matchRecord.notOnPath(yi)) {
                matchRecord.setOnPath(yi, true);
                if (matchRecord.getAugmentPath(yi) == -1
                        || findAugmentPath(matchRecord, matchRecord.getAugmentPath(yi))) {
                    matchRecord.setAugmentPath(yi, xi);
                    return true;
                }
            }
        }
        return false;
    }

    private static void print(MatchRecord rec) {
        int[] aug = rec.getAugmentPath();
        System.out.println("匹配结果: ");
        System.out.println("y  --  x");
        for (int yi : aug) {
            System.out.println("" + yi + " <--> " + aug[yi]);
        }
    }
}

最终输出结果:

匹配结果:
y  --  x
0 <--> 0
2 <--> 1
1 <--> 2

最后

以上就是匈牙利算法, 不过上面我们解决的仍是无权匹配的问题, 下篇博客我们将讨论有权匹配的问题和相关算法.

参考

匈牙利算法
 图论(匹配)
https://www.renfei.org/blog/bipartite-matching.html