Up / Down 排序

在 web 应用中我们经常会涉及到排序, 比如根据用户对某些 item 的喜恶等进行排序, 其中核心就是排序的方法.

常见的方法:

方法1, 根据 喜好的人数 - 不喜欢的人数 的结果进行排序, 常见的是 Up 和 Down 投票.
假设 ItemA 有 100 Up 和 40 Down, ItemB 有 550 Up 和 450 Down, 如果根据 Up-Down 的结果进行排序, 那么 B 将先于 A.
这种方法偏向于绝对的投票数, 但却忽略了好评率.
方法2, 使用 喜欢的人数/投票人数 , 但这种方法不适合投票人数很少的情况.

那有没有更好的排序方法呢 ?

二项分布和样本估计

由于每个用户的投票都是独立事件, 每个投票只能选择Up或者Down, 这就像统计学中的二项分布.

由于投票的用户只是总体用户的一部分, 因此我们本质是也是想用样本估算总体, 近似估计全部用户的打分.

那么, 这就将涉及到置信区间.

由于使用样本估计总体结果的可信度是值得怀疑的, 因此, 统计学上用置信水平和区间来进行衡量估计的可信度.

例如, 我们有95%的把握相信整体好评率在 [75, 85] 这个区间, 95%是置信水平, 75-85则是置信区间.

样本少, 置信区间则比较宽, 下限也比较低. 因此, 我们可以通过这个置信下限对每个 item 进行排序.

为了求解置信区间, 在统计学上, 一般使用正态分布来近似求解二项分布, 然而需要满足 np > 5 和 nq > 5 的情况.

因此, 当样本比较小的时候, 这样就有局限性.

威尔逊区间

美国数学家 Edwin Bidwell Wilson 提出了一个公式，为了解决了小样本的问题, 我们称之为 "威尔逊区间" .

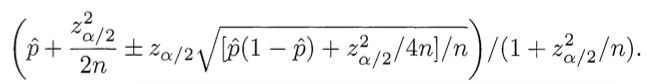
其中, p-hat 为赞成概率, n 为样本大小, z 为某个置信水平的 z-score 常数(可以查表得到)

写成函数就是:

from math import sqrt


def wilson_bound(p, n, z=1.96):
    denominator = 1 + z ** 2 / n
    centre_adjusted_probability = p + z * z / (2 * n)
    adjusted_standard_deviation = sqrt((p * (1 - p) + z * z / (4 * n)) / n)

    lower_bound = (centre_adjusted_probability - z * adjusted_standard_deviation) / denominator
    upper_bound = (centre_adjusted_probability + z * adjusted_standard_deviation) / denominator
    return (lower_bound, upper_bound)

参考

基于用户投票的排名算法（五）：威尔逊区间 - 阮一峰的网络日志
 How Not To Sort By Average Rating – Evan Miller
https://www.mikulskibartosz.name/wilson-score-in-python-example/