什么是 Jaccard (雅卡尔) 系数

Jaccard 系数主要用于计算两个集合之间的相似度(比如用于新闻和论文查重等), 定义为两个集合交集大小与并集大小之间的比例:

然而, 要将这个公式转化为实际计算, 还存在一些问题, 尤其是计算海量数据时.

如何方便的计算相似度

第一个要处理的问题就是如何方便的计算 Jaccard 相似度, 首先需要提到 minhash, 通过这个我们可以快速的估算相似度.

假设有以下数据, 集合S1={a,d}, S2={c}, S3={b,d,e}, S4={a,c,d}, 我们首先用以下矩阵表示 (暂且称为集合矩阵) :

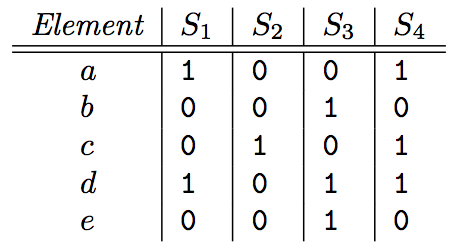
然后我们对这个矩阵的 row 进行随机的重排列 , 假设随机后得到以下的新矩阵:

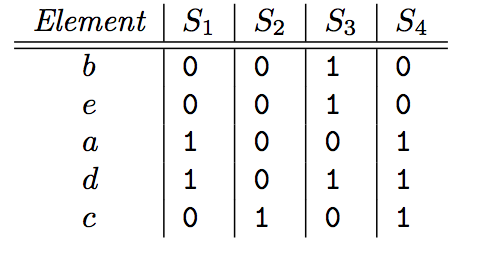
然后我们记录每个集合的 minhash, 这个 minhash 就是每个集合(列方向)上遇到的第一个值为1的行索引.

也就是 minhash(S1)=a, minhash(S2)=c, minhash(S3)=b, minhash(S4)=a.

那么之后, 我们可以利用以下的性质进行 jaccard 相似度的计算:

The probability that the minhash function for a random permutation of
rows produces the same value for two sets equals the Jaccard similarity
of those sets.
对于一个随机的行排列，两个集合的 Jaccard 相似度等于两个集合的 minhash 相等的概率.

这个推导过程可以参考 <Mining of Massive Datasets> 书里的 3.3.3 Minhashing and Jaccard Similarity 部分.

重排列的问题

由于现实中要重排列海量的row也是不太可行的, 这个计算和时间开销是巨大的.

为了解决这个问题，我们通过一些随机哈希函数达到随机排列行的效果. 好像很厉害的样子, 具体做法如下.

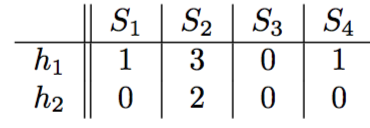
例如, 假设我们只选择 2 个 hash 函数(x+1 mod 5 和 3x+1 mod 5)对上面的集合矩阵进行排列, 我们分别命名为 h1 和 h2 , 并将集合矩阵中的 abcde 换成行号, 用 x 表示.

对于某一行, 然后我们假设 SIG(i,c) 为第i个hash函数第c列的值, 然后进行以下操作:

Initially, set
SIG(i, c) to ∞ for all i and c. We handle row r by doing the following:
1. Compute h1 (r), h2 (r), . . . , hn (r).
2. For each column c do the following:
(a) If c has 0 in row r, do nothing.
(b) However, if c has 1 in row r, then for each i = 1, 2, . . . , n set SIG(i, c)
to the smaller of the current value of SIG(i, c) and hi(r).

即我们从 row=0 开始遍历到 row=4, 当处理某一行 r 时:

如果某个集合 S 的值为 1 时, 才把 SIG(i,c) 的值设置到 SIG矩阵; 否则不操作.
如果要设置 SIG矩阵中对应位置已经有值, 则选择更小进行填充.

最终得到的 SIG矩阵如下 :

SIG(1,1)为1, 是因为 row=0,h1=1, 此时h1的值最小.
SIG(1,2)为3, 是因为 row=3,h1=3, 此时h1的值最小.
SIG(1,3)为0, 是因为 row=4,h1=0, 此时h1的值最小.
SIG(1,4)为1, 是因为 row=4,h1=0, 此时h1的值最小.

这样，我们可以把集合矩阵的 N 行压缩到SIG矩阵的 n 行, n 为 hash 函数的个数, 比如这里的集合 S 已经从 5 个元素的向量变成了 2 个元素的向量.

两两比较的问题

但是现在还有一个问题, 我们需要计算S集合两两之间的相似度, 这依然是一个很大的计算量.

一个思路是尽量减少参与的集合数, 从而减少计算量.
LSH 就是其中一个方法. LSH (Locality-Sensitive Hashing), 是预先将低相似度的S集合过滤掉, 只计算高于阈值的相似度的S集合, 从而减少计算量. LSH 的方法如下.

假设有一个 12 行的签名矩阵, 我们把它分为 4 个 band, 每个 band 由 3 行组成. 即一个12元素的列向量, 会被切成4份, 每份有3个元素.

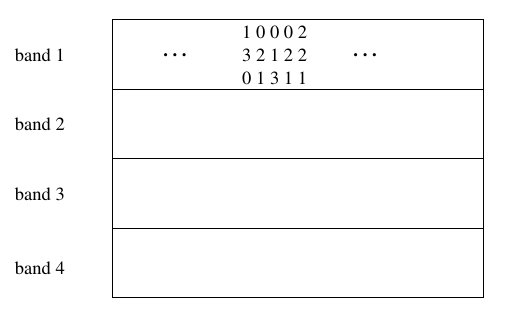
如上, 当处理第一个 band 时, 由于第2列和第4列都有相同的列向量 [021], 所以这两列会落在 hash 之后会落在同一个桶里, 同一个桶的列将会称为候选对, 参与到后续的相似度计算.

每一个 band 都有独立的桶数组, band 1 处理完后, 接着看 band 2, 如此下来, 在所有 band 中都无法 hash 到同一个桶的列, 则被认为是低相似度的, 不参与后续计算.

由上可知, LSH 可以找出相似度高的集合, 但不适用于计算所有文档的相似度.

参考

书 : <Mining of Massive Datasets>
https://blog.csdn.net/u011467621/article/details/49685107
https://blog.csdn.net/liujan511536/article/details/47729721