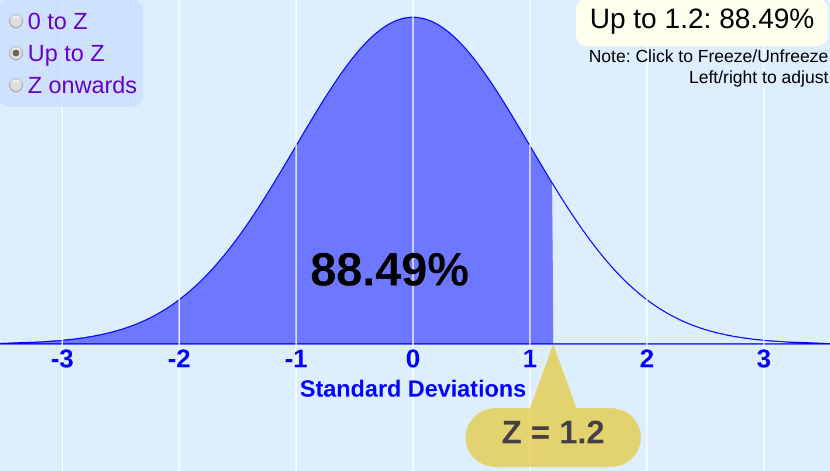
假如你有一个比较大的样本(比如大于30), 那么你可以直接计算 z-score 来检验结果是否显著.
定义
假设一个 AB 实验有 A和B 两组, 人数都为 N = 2000 , $\hat{R_a}$ 为 A组的转化率(为7%), $\hat{R_b}$ 为 B组的转化率(为8%).
由于总体 $A \sim B(N, R_a)$, 总体 $B \sim B(N, R_b)$ ,
根据中心极限原理, 此时样本 $\hat{R_a}$ 和 $\hat{R_b}$ 近似服从正态分布.
检验什么
而在双样本实验里, 我们假设 B 比 A 好, 即 $R_a<=R_b$, 即 $R_b-R_a>=0$ , 我们检验实验效果是否显著, 也就是看这个假设概率有多大.
样本比例 Ps 的分布
我们用 $P_s$ 代表样本比例这个随机变量, 如果样本 n 够大(比如n>30), 则:
$$P_s \sim N(p, \frac{pq}{n})$$
应用到我们的场景, $P_s$ 为:
$\hat{R_a} \sim N(\hat{R_a}, \frac{\hat{R_a}(1-\hat{R_a})}{N})$
$\hat{R_b} \sim N(\hat{R_b}, \frac{\hat{R_b}(1-\hat{R_b})}{N})$
那么, $\hat{R_b}-\hat{R_a} \sim N(\hat{R_b}-\hat{R_a},\frac{\hat{R_a}(1-\hat{R_a})}{N}+\frac{\hat{R_b}(1-\hat{R_b})}{N})$ .
(注意这里的方差是相加, 不是相减)
检验
由于我们假设 $R_b-R_a=0$, 均值为0, 方差为: $(\frac{\hat{R_a}(1-\hat{R_a})}{N}+\frac{\hat{R_b}(1-\hat{R_b})}{N})$, 根据 $Z=\frac{X-\mu}{\sigma}$ 得到 :
$Z = \frac {\hat{R_b}-\hat{R_a}-0} {\sqrt{\frac{\hat{R_a}(1-\hat{R_a})}{N}+\frac{\hat{R_b}(1-\hat{R_b})}{N}}}$
Z 计算得到 1.2008168332644198 .
再计算 显著性水平5% 对应的 $Z_\alpha$ 为: 1.64 , 因此不能认为 B 组显著比 A 组好.