前面用 Pregel API 实现 sssp 的例子可能比较简单, 但用 Pregel 也可以实现 PageRank.

PageRank 是什么

PageRank 是早期 Google 搜索引擎中对网页排名的一种算法, 该算法以 Google 创始人之一的 Larry Page 的名字来命名.
其核心思想是被其他网页引用更多的网页, 重要性越高.

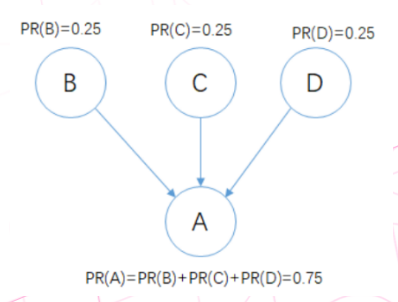
如上图, 有4个顶点, 每个顶点是一个网页, 顶点 D 到 A 的有向边表示, D网页引用了 A 的地址链接, 从D网页可以到达A网页.
现在我们用 PR 来表示一个用户点击某个网页的概率. 因为这里有 4 个顶点, 所以一开始的话每个结点都是 1/4=0.25 的概率.
接着, 由于从 BCD 都可以到达 A 的地址, 那么 PR(A) 的概率则等于 BCD 的概率之和, 所以 A 的 PR值就被更新为 0.75 .

通用的, PR 的计算公式可以如此定义:

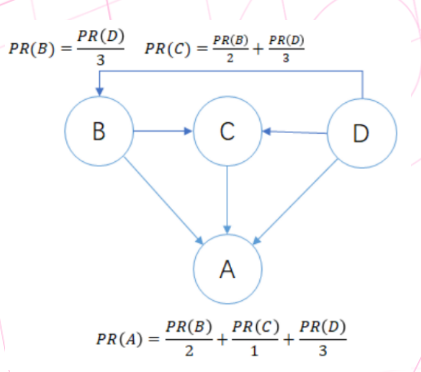
分子是源顶点的PR值, 分母是源顶点的出度.
例如 PR(B), 顶点B 的源顶点只有一个顶点D, 顶点D有 3 个出度, 因此 PR(B) = PR(D)/3.
PR(C), 顶点C 的源顶点有两个: 顶点B和顶点D, 顶点B有 2 个出度, 顶点D有 3 个出度, 因此 PR(C) = PR(B)/2 + PR(D)/3.
PR(A) 计算同理.

但是由于现实中一个随机点击链接的网上冲浪者最终会停止点击, 而不是一直浏览下去。所以, PageRank 定义了一个 damping factor 阻尼系数d, 代表这个人继续前进的概率。各种研究测试过不同的阻尼系数，通常设置阻尼系数在 0.85 左右. 于是上面的 PR 值公式可以改为:

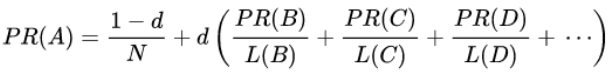
其中 N 为顶点数目.

GraphX 中的 PageRank

那么 GraphX 中的 PageRank 是如何实现的呢 ?
我们打开 org.apache.spark.graphx.GraphOps#pageRank 源码:

def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double] = {
  PageRank.runUntilConvergence(graph, tol, resetProb)
}
def runUntilConvergence[VD: ClassTag, ED: ClassTag](
  graph: Graph[VD, ED], tol: Double, resetProb: Double = 0.15): Graph[Double, Double] =
{
    runUntilConvergenceWithOptions(graph, tol, resetProb)
}

核心代码在 runUntilConvergenceWithOptions() 中 :

val pagerankGraph: Graph[(Double, Double), Double] = graph
  // Associate the degree with each vertex
  .outerJoinVertices(graph.outDegrees) {
    (vid, vdata, deg) => deg.getOrElse(0)
  }
  // Set the weight on the edges based on the degree
  .mapTriplets( e => 1.0 / e.srcAttr )
  // Set the vertex attributes to (initialPR, delta = 0)
  .mapVertices { (id, attr) =>
    if (id == src) (resetProb, Double.NegativeInfinity) else (0.0, 0.0)
  }
  .cache()

val initialMessage = if (personalized) 0.0 else resetProb / (1.0 - resetProb)

def vertexProgram(id: VertexId, attr: (Double, Double), msgSum: Double): (Double, Double) = {
  val (oldPR, lastDelta) = attr
  val newPR = oldPR + (1.0 - resetProb) * msgSum
  (newPR, newPR - oldPR)
}

def sendMessage(edge: EdgeTriplet[(Double, Double), Double]) = {
  if (edge.srcAttr._2 > tol) {
    Iterator((edge.dstId, edge.srcAttr._2 * edge.attr))
  } else {
    Iterator.empty
  }
}

def messageCombiner(a: Double, b: Double): Double = a + b

val vp = if (personalized) {
...
} else {
  (id: VertexId, attr: (Double, Double), msgSum: Double) =>
    vertexProgram(id, attr, msgSum)
}

Pregel(pagerankGraph, initialMessage, activeDirection = EdgeDirection.Out)(
  vp, sendMessage, messageCombiner)
  .mapVertices((vid, attr) => attr._1)

可以发现, 其实里边也是通过 Pregel API 来做的:

首先, 对 graph 进行预处理, 主要是计算顶点出度数, 然后更新 edge 的 weight 为 1/出度数 , 并设置顶点的初始值, 得到新的图 pagerankGraph .
之后就是定义之前提过的 Pregel 需要的 3 个业务函数: vertexProgram , sendMessage, messageCombiner. 这 3 个函数定义的 Pregel 过程, 其实就是迭代计算 PageRank 的值, 也就是前面的 PageRank 公式.
resetProb: Double = 0.15 这个值是公式里的 1-d.
vertexProgram 可能看不太懂, 因为有个值 msgSum 来自其他结点, 需要先看 sendMessage 和 messageCombiner, 再回来看 vertexProgram.
sendMessage 中, edge.srcAttr._2 是 vertexProgram 中的 delta: newPR - oldPR, 将和 tol 对比作为是否继续迭代发送消息的条件. edge.attr 就是预处理的 edge 的 weight : 1/出度数, 因此 edge.srcAttr._2 * edge.attr 就等于 delta/出度数 .
messageCombiner 合并消息的逻辑就是进行加法合并. 因此, 回到 vertexProgram, newPR 其实等于: oldPR + sum(delta/出度数). 可以发现对比 PageRank 公式不同的一点是 : GraphX 中的 initialMessage 用的是 resetProb / (1.0 - resetProb).

如此 PageRank 将会一直迭代计算, 直到达到 tol 控制的收敛条件为止, 我们设置的 tol 值越小, 则结果越精确.

例子

最后, 给一个官方 example 的运行结果, 我用 python 进行了可视化:

https://github.com/apache/spark/blob/master/examples/src/main/scala/org/apache/spark/examples/graphx/PageRankExample.scala

可以看到, 只有一个出度的顶点1 是PR值最高的.

参考

https://blog.csdn.net/a358463121/article/details/79342109