常见指标
- error rate (E): 假设有 m 个样本, 其中 a 个样本分类错误, 那么
E=a/m - accuracy (classification 领域) : 等于
1 - a/m
precision 和 recall
这两个是 information systems 领域的定义, 比如 web search engines.
- precision (查准率or准确率) : $P = \frac {True Positive} {预测为 Positive 的样本数} = \frac {True Positive} {True Positive + False Positive}$.
- recall (查全率or召回率) : $R = \frac {True Position} {真实为 Positive 的样本数} = \frac {True Positive} {True Positive + False Negative}$,
False Negative即是被预测为 Negative 的 但其实为 Positive 的样本.
更直观的, 以二分类任务结果的 confusion matrix (混淆矩阵) 为例:
| - | 预测为 Positive | 预测为 Negative |
|---|---|---|
| 真实为 Positive | True Positive | False Negative |
| 真实为 Negative | False Positive | True Negative |
以上四种情况的预测结果对应的样本数, 加起来就是样本总数.
假设任务是在一堆西瓜中挑出好瓜, 那么 precision 相当于: 我们挑出来的认为的好瓜中 有多少是真的好瓜, recall 相当于: 所有好瓜中有多少被我们挑出来了.
例如100个西瓜, 总共有30个好瓜, 我们逐个检查之后挑出来20个自认为的好瓜, 然而其中10个才是真正的好瓜, 那么 precision = 10/20 = 50%, recall = 10/30 = 33%.
precision 和 recall 是一对矛盾的指标.
例如, 想要较高的 precision, 那么只选1个自认为最有把握的好瓜, precision 将会是 100%, 然而 recall 将会很低(1/30=3%), 我们漏掉了不少好瓜;
例如, 想要较高的 recall, 那么把100个瓜都选为好瓜, recall 将会是 100%, 然而 precision 将会很低.
场景换到搜索引擎等等应用上也是常见的.
如果把学习器按 Positive 可能性从高到低排序, 然后把它们逐个作为 Positive 预测结果, 那么可以得到这样的 P-R 曲线 (Precision-Recall) :
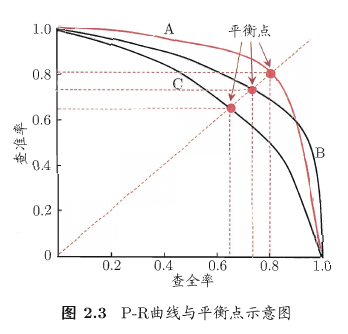
(图片来自<机器学习>周志华)
比较两个学习器:
如果一条 P-R 曲线能够完全包住另一条 P-R 曲线, 那么可以说前者的性能由于后者.
有交叉时, 也可以比较曲线下的面积, 但是不好估算.
还可以用 Break-Event Point (BEP) 平衡点, 比较 Precision=Recall 时的取值.
F1 值
不过常用的是 F1 值, $F1 = \frac {2 \times P \times R} {(P + R)} = \frac {2 \times TruePositive} {样例总数 + TruePositive - TrueNegative}$
F1 的通用形式是 $F_\beta = \frac{(1 + \beta^2) \times P \times R}{(\beta^2 \times P) + R}$, $\beta > 0$
$\beta = 1$ 时即是 F1, $\beta < 1$ 时, precision 有更大影响, $\beta > 1$ 时, recall 有更大影响.
ROC
ROC (Receiver Operating Characteristic), 和前面提到的 P-R 曲线类似, 只不过 ROC 曲线的纵轴是 $TruePositiveRate = \frac {True Positive} {True Positive + False Negative}$, 即真实为Positive的样本中有多少是预测为Positive的, 横轴是 $FalsePositiveRate = \frac {False Positive} {False Positive + True Negative}$, 即真实为Negative的样本中有多少是预测为Positive的.
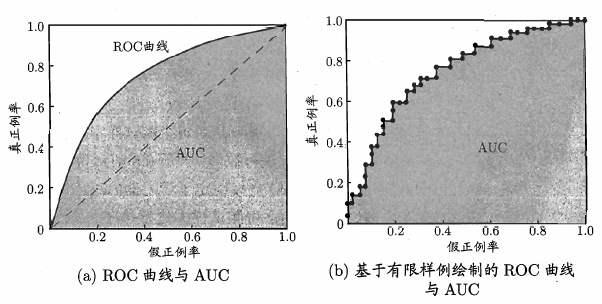
(图片来自<机器学习>周志华)
其中 AUC (Area Under ROC Curve), 是对 ROC 曲线下面的面积求和而得到的.
Cost Curve 代价曲线
现实中, 模型预测往往会出现错误, 比如 False Negative 和 False Positive 的结果, 但是不同场景下这些错误付出的代价可能不一样.
前面我们都假设二者的代价是均等的, 在非均等代价时, ROC 曲线不能直接反应出期望总体代价, 这时就需要 Cost Curve 曲线了.
假设 $cost_{01}$ 为 False Negative 的错误代价, $cost_{10}$ 为 False Positive 的错误代价, p 为样本是 Positive 的概率, 那么归一化代价 $cost_{norm}$ 就等于:
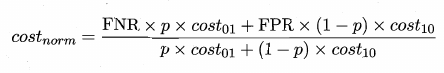
由于 FNR = 1 - TPR, ROC 曲线某个点的坐标为(TPR, FPR), 可就是 FPR 和 FNR 这两个数据都可以从 ROC 曲线获得, 对于 ROC 曲线上的1个点可以绘制出对应的一条从(0, FPR) 到 (1, FNR) 的线段, 所有点对应的线段围起来的下界面积 就是期望总体代价.
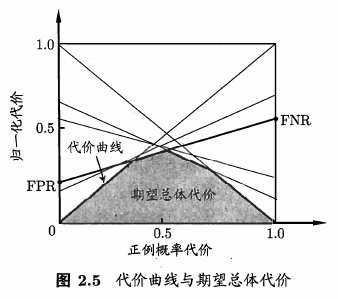
(图片来自<机器学习>周志华)
偏差-方差 分解
- 模型输出和真实标记之间的差别称为
bias(偏差). - 不同训练集学习到的模型的输出结果很可能不同, 即使是同一分布, 这些模型输出值之间的差别称为
variance(方差).
假设一个模型为一个点, 那么有几种可能, 如下图:
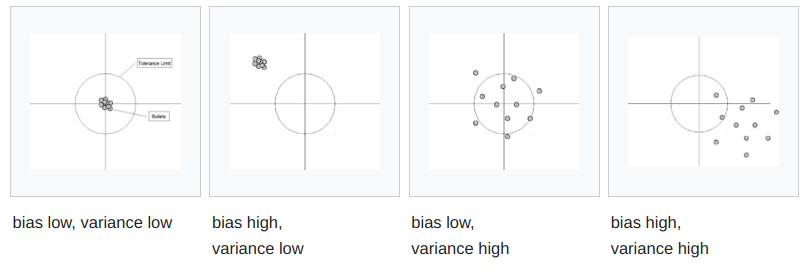
我们都想要 low bias low variance, 但往往 bias 和 variance 是鱼和熊掌, 可以参考这张图 (其中泛化误差可以认为是 bias 和 variance 和 噪声 之和) :
Bias–variance tradeoff - Wikipedia
对于 bias 和 variance 的关系, 一个类比就是测量学中的 accuracy 和 precision (这里是测量学的概念, 根据 ISO 的定义; 前面提到的 accuracy 和 precision 则是 classification 领域和 information systems 领域的定义, 不要混淆了喔, Wiki 中也有介绍):
accuracy 是测量值和真实值之间的接近程度.
precision 则是在不变条件下重复测量显示出相同结果的程度.
如果拿一组测量值来说, accuracy 关注点在于这些测量值的平均值, precision 关注点在于这些测量值的标准差.
参考
周志华 <机器学习>