ChatGPT 的火热
最近 ChatGPT-3 一直占据着媒体的头条, LLM 大语言模型在达到一定规模时的能力涌现, 确实很惊艳, 前几年学习了解深度学习时, 对其 NLP 的效果还是觉得差强人意, 但是这次的确给人带来惊喜, 在很多领域可以带来生产力的提升.
ChatGPT 是基于 Transformer 的, 2017年在学习 Deep Learning 时, 主要是看 Andrew NG 的资料, 那时的 DeepLearning.ai 课程还没有 Transformer 内容, 毕竟 Transformer 才刚出来, 后来才新增了这部分内容(Transformer Network), 所以没怎么仔细看, 今天得重新了解一下 Transformer.
Self-Attention
首先, 从 Self-Attention 开始, 以 Andrew 中的 法语翻译为英语 为例, 来了解什么是 Self-Attention, 如下图:
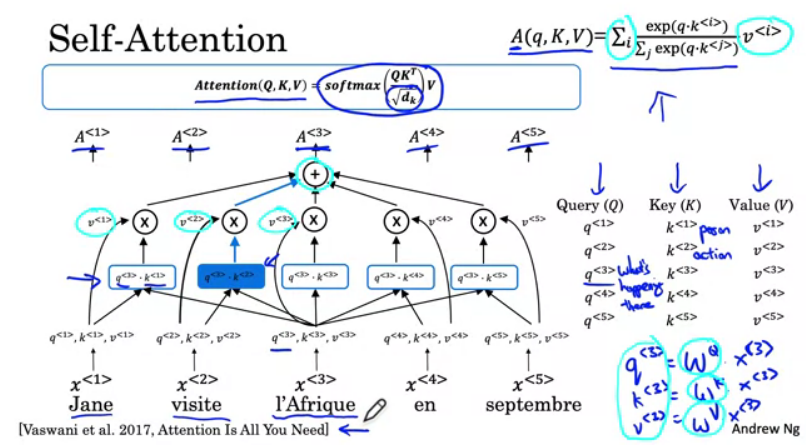
首先我们定义 A(q, K, V) 为 一个基于 Attenttion 的 word 的向量表示, X 为输入.
假设现在输入法语 Jane visite l'Afrique en septembre, 则
$x^{<3>}$ 代表 l'Afrique ,
$q^{<3>}$ 等于 $W^Q \cdot x^{<3>}$ ,
$K^{<3>}$ 等于 $W^K \cdot x^{<3>}$ ,
$V^{<3>}$ 等于 $W^V \cdot x^{<3>}$ ,
那么, $A^{<3>}$ 的计算过程如下所示.
1. 计算 $q^{<i>} \cdot k^{<i>}$
首先是 $q^{<3>}$, 它可能代表了比如 What is happening there 这样的问题, 因为 l'Afrique 是一个地点, 所以当计算 $A^{<3>}$ 时, 你想知道 What is happening there.
那么接下来要做的是:
- 计算 $q^{<3>} \cdot k^{<1>}$, 这可能代表了 $x^{<1>}$ 如果作为
What is happening there这个问题的答案, 有多好 - 类似的, 计算 $q^{<3>} \cdot k^{<2>}$, 接着 $q^{<3>} \cdot k^{<3>}$, 接着 $q^{<3>} \cdot k^{<4>}$ 等等
假如 $k^{<1>}$ 代表 Person, $k^{<2>}$ 代表 Action, 那么 $q^{<3>} \cdot k^{<2>}$ 将会有最大的值, 因为直觉上 visite 给出了 What is happening there 这个答案最相关的 Context, 即 l'Afrique 将会被 visite.
接着, 计算 Softmax, 由 Softmax 公式:
$\sigma(z_i) = \frac{e^{z_{i}}}{\sum_{j=1}^K e^{z_{j}}} \ \ \ for\ i=1,2,\dots,K$
代入可得 A(q, K, V) 公式的一部分:
$\frac{exp(q \cdot k^{<i>})}{\sum_{j} exp(q \cdot k^{<j>})}$
2. $v^{<i>}$ 和 Sum
接着, $q^{<i>} \cdot k^{<i>}$ 的 Softmax 乘以 $v^{<i>}$, 然后进行 Sum, 于是得到了 A(q, K, V) 公式 :
$\sum_{j} \frac{exp(q \cdot k^{<i>})}{\sum_{j} exp(q \cdot k^{<j>})} v^{<i>}$
如此, 可以计算得到 $A_{<3>}$, 类似计算可得到 $A_{<1>}$, $A_{<2>}$, $A_{<4>}$ 等等.
在论文 <Attention Is All You Need. 2017> 里的向量表示的公式为:
$Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt[2]{D_k}})V$
可以发现多了一个 $\sqrt[2]{D_k}$ , 它一般是 Key Vectors 的 dimension 的平方根, 目的是进行 scale 以防止数值 explode, 它可以让算法有更稳定的梯度.
Next
这就是 Self-Attension 的结构, 通过每个 word 的 Query Key 和 Value 三者, Query 让我们问关于该 word 的一个问题, Key 来帮助查看所有其他 words, 检查和 Query 的相似性, 找到和 Query 问题的答案最相关的 word, 最后 Value 允许 Key 集成和表示在该 word 的特征 $A$ 之中, 比如 visite ($k^{<2>}$) 在 l'Afrique 对应的 Representation $A^{<3>}$ 中.
BTW, 这种类型的 Attention, 还有一个名称叫做 The Scaled Dot-Product Attention.
了解完 Self Attention, 接着就可以看 MultiHead Attention 了.