以前在学习 Lucene 和搜索引擎原理时, 了解过 Vector Space Model + tf_idf,
不过今天的主角是用户兴趣挖掘, 是因为之前发现有些公司这样用了.

tf_idf

首先了解什么是 tf_idf.

在文本搜索引擎中, 我们一般会输入多个词语进行搜索(暂且把一个词语称为 term, 严格来说是不完全相等),
那么如何评估一个词语 term 和一个网页 document 的相关性呢?
最直观的, 就是这个 term 在这个 document 中出现的次数, 次数越大, 相关的可能性越大.
这就是 Term Frequency, 用 $tf_{t,d}$ 表示.

但是, 有些 term 的 tf 高, 不代表越相关. 比如一些常用词, 广泛分布在大部分文档中.
这就需要用到 Inverse document frequency (idf) 了, 最简单的版本 :
$idf_t = log \frac{n}{df_{t}}$ .

${df_{t}}$ 是 document frequency, 表示有多少文档包含了这个 term.
$n$ 是总的文档数目.

(上面的 idf 公式在实际使用中会进行修改, 比如避免 division-by-zero 的问题)

这样, 我们结合 $tf$ 和 $idf$ 来表示一个 $term$ 和 $document$ 的相关性 :
$Weight_{t,d} = tf_{t,d} \times idf_t$

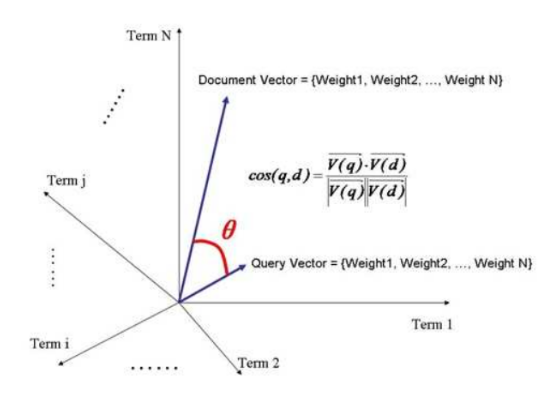
Vector Space Model

上面是一个 term 的情况, 如果有 $m$ 个 $terms$, 相应的也有 $m$ 个 $Weight_{t,d}$,
在这 $m$ 个 $Weight_{t,d}$ 的空间里组成的一个向量 $Vector_d$,
可以表示一个 document 和 terms 之间的相关性.
同样, 我们的查询语句在这些 terms 空间中, 也能组成一个向量 $Vector_q$.
$Vector_d$ 和 $Vector_q$ 夹角的 cos() 值越大, 那么就可以表示两个 Vector 的相似性越大.
这就是 Vector Space Model :

应用于用户兴趣挖掘

短期兴趣

以浏览网页为例, 如果把 $term$ 替换为兴趣标签, 把 $document$ 替换为一天中浏览的所有网页标签的集合,
那么 $n$ 则等于统计周期的总天数, 某个兴趣标签某天的 $tf$ 等于用户当天该兴趣标签的频次,
$df$ 则等于该标签被浏览的天数, 至此可以得到该标签的 $Weight$.
同理, 用户浏览的每个标签都能得到一个 $Weight$, 这样可以进行一个排序,
作为用户兴趣用于各项业务中(比如个性化推荐等等).

由于每个标签每天都对应一个 $Weight$, 对于短期兴趣来说, 越近的一天, 标签的 $Weight$ 应该越高.
假设以近七天作为短期兴趣的统计周期, 每一天的 $Weight$ 在相加时,
需要设置不同的权重值, 使得近期的 $Weight$ 发挥更大作用.

兴趣相似的人

由于兴趣标签进行了排序, 可以根据某个标签找相同兴趣标签分值大的人.
也可以根据这些标签 $Weight$ 组成的 $Vector$, 寻找相似的人, 类似文本搜索相似性的计算.

把 Vector Space Model 和 tf_idf 用于用户兴趣挖掘的想法挺有趣的, 之前学习 Lucene 的知识还这样用上了.

参考

https://en.wikipedia.org/wiki/Tf%E2%80%93idf
基于VSM模型的移动互联网用户兴趣度挖掘分析和应用--《电信技术》2018年02期